nr. 978 - Tents and trees

The last puzzle is a Tents variation. In this variation you have to find the trees, too.
The genre appeared on the WPC2003, Arnheim. It was the team puzzle of the first weakest link. Its size was 10x10. When I finished the individual puzzle after 40 minutes, (I was in top20 with this solving time :), and I was the first Hungarian in the center.) I got a 5x5 corner. You can imagine that it didn't provide me any information. The 2nd player brought another useless corner.  We could start solving when the 3rd part arrived. And it was possible to solve the whole puzzle without the 4th part. But I realized this just after the round, of course.

This is a hard puzzle type, so usually a 6x6 grid is enough for magazines or competitions. This puzzle is solvable logically. But I think you need to know really well the Tents solving technics.

Rules for Tents and Trees

More puzzles from this genre


This is the last puzzle from the mini series. I hope you enjoyed them.

Yesterday I solved some of my old Dutch loop puzzles. I especially enjoy the loop puzzles which don't use all cells. You can find these puzzles here, they are small:
Dutch loop
Masyu

Rules: Tents and trees

Place some trees and tents into the grid. Each tree in the figure has a tent attached to it that has to be in an edge-adjacent cell. Trees do not touch each other, not even diagonally, and the same goes for the tents. Numbers outside the grid indicate the number of tents and trees in that row or column.

nr. 979 - Coralfinder

I continue the mini week with 2 more puzzles. But they are even smaller :)

Today's puzzle is my first invention. I thought of this puzzle type in 2001.

This puzzle solvable logically, but the guessing is also an effective way.

Rules for Coralfinder

Rules: Coralfinder

Select a connected set of squares - the coral - so that it does not touch itself, not even diagonally. (It means that the coral can have no island inside itself.) Numbers outside the grid indicate the lengths of consecutive parts of the coral in the given row or column (similary as in the "Paint it black" puzzles). However, numbers belonging to the same row or column are in increasing order and not in the order they appear. No 2x2 area may be covered by the coral.

nr. 980 - Dutch loop

Friday puzzle is a Masyu version. In the Masyu the black circles provide strong starting points. In this variation the rules are weeker.

I can't explain the puzzle name. It appeared in a Hungarian puzzle book (published in 2001) under this name. So normally I use this title.

Rules for Dutch loop

Rules: Dutch loop

Draw a single, non-intersecting loop that passes through all circled cells. The loop must go straight through the cells with white circles, and must make a turn in all the black circles.

nr. 981 - First Seen Coral

I tried to create a small, antisymmetrical Coral puzzle. After a lot of suffering I finished this puzzle, and it was harder than I expected :) Nevertheless this is the easiest puzzle of the week, but it provided the idea that I should create some more similar puzzles.

Rules for First Seen Coral

Rules: First Seen Coral

Fill in some cells to create a connected shape which does not touch itself, not even diagonally, and does not contain 2x2 fully filled cells. The corral cannot have an island inside it. The clues outside the grids represent the length of the first filled cell block in that direction.

nr. 982: Pentopia

I like a lot the pentomino puzzles. They are not tipically small puzzles. But the Pentopia can be an exception :-) So this is the 3rd (and my favourite) puzzle of the series. It's a special a bit, because all clue cell has exactly 2 arrows.

Rules for Pentopia

Rules: Pentopia

Place pentominos in the grid without repeating any shape. Rotations and reflections are considered the same shape. The pentominos are not allowed to touch, not even at the corners. The lines in the grid indicate the direction(s) in which the pentominos is/are closest when looking from that square.

nr. 983: Lakes

The second puzzle is a Nurikabe variation.

Rules for Nurikabe
In this variation there isn't extra rule about the painted squares. They can contain 2x2 area and they don't have to be connected.

Nurikabe has a lot of names. One of them is the Stream Islands (Puzzle Picnic). It is a good name, because the painted squares form a river. Now they are just separeated parts hence I use the Lakes title. (I don't know if the puzzle variation has a regular English title.)

This is a common puzzle type in the Dutch puzzle magazine, Breinbrekers. The size is always huge, but the puzzles are really easy. This puzzle is the counterpoint of that style :)

If you liked this puzzle, you can solve some of my old puzzles from the genre here.

Rules: Nurikabe

Determine for each cell if it's part of the stream or an island. Each number is part of a single island of horizontally and vertically connected cells, which size is equal to that number. Islands can't touch eachother horizontally or vertically. The cells not part of an island form the stream. The stream is a single connected area, which doesn't cover any 2x2 areas anywhere.

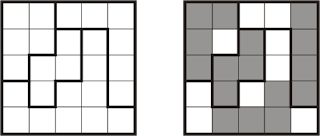
nr. 984 - LITS

I love the small but not too easy puzzles. An extreme example is the Arrows puzzle of the WPC2011. It was only 2x2 and the number of possible positions of arrows around the grid is only 64. But the solving time was 2 or 3 minutes and only 50% of the participant solved it.

This week I will publish some small puzzles. But generally they will be harder than you expect, however, there is a natural limit of difficulty because of the limited size. Sometimes it took me a lot of time to gain 1 or 2 minutes more. Is it worth? Generally no, but sometimes I can create / discover a gem. :-)

The first one is a LITS.

Rules for LITS

Rules: LITS

Colour a shape of 4 orthogonally connected squares in each black bordered region so that all coloured squares form a single contiguous area. This area can't contain any 2x2 coloured squares. Two identical shapes in different regions can't touch eachother by a side. Rotations and reflections are considered the same shape.